10,000 Nights at a Casino – Revisted

I don’t really want to spend anymore time on what I thought was an interesting but somewhat fruitless exercise.  However, there seems to be some misconceptions about my last post on using Python to test a basic roulette strategy.  And, I have gotten some people saying that there is no possible way for the roulette strategy I outlined to have a positive expected outcome.

The arguments I received were mostly “well, if that is true, then why isn’t everyone doing it?”  Personally, I think that is a terrible reason for disqualifying anything.  This mindset reminds me of the efficient market hypothesis (EMH) we were taught in school. This theory basically states that all information regarding a stock is going to be available to the general market and thus priced into the stock.  The overarching theory is that generally there are no opportunities to make “outsized returns” – meaning beyond the average, unless you get lucky.  I think that the capital markets in particular have shown this theory to be outdated and ridiculous.  This is besides all of the interesting businesses/people that have made “outsized returns” even in markets that were mature.  But in this case, EMH may hold true as there is no way to make outsized returns on this game without a bit of luck.  Regardless of the validity of this argument, I personally prefer theses grounded in quantitative analysis where possible – and this is definitely a situation where numbers are applicable and available.

To make one thing clear: my theory, which I likened to picking up nickles in front of a steam roller, isn’t necessarily one that I would employ.  However, I thought it was an interesting thought experiment (and by no means an original idea as Dave pointed out in the comments).  I also thought it was a good basis to explain some interesting concepts and introduce Python.  I’ll focus this post on probability theory, once again using my strategy as an example.

It is impossible to gain an advantage in a game where you are expected to lose on a case by case basis.  Meaning, if you bet $1 on black, you should expect to get back less than $1 on average.  Sometimes you will win and come away with a $1 profit, but more times you will lose and come away with $0.  Specifically, your chances of winning are 47% (18 possible winning outcomes/38 possible outcomes), and your chances of losing are 53% (20 possible loser outcomes/38 possible outcomes).  So, your expected profit (which is defined as the average returns you would expect to get if you did this bet infinity times) would be ($1 * 47%)+(-$1*53%) which is about -$0.05.  This is how casinos make money.  You bet the same amount each time and they win, on average.  In this case, they will, on average, win 5.5 cents on each spin.

So, my strategy is to double your bet when you lose.  But, that means you are just spinning again, with more money on the table, and thus an even greater expected loss.  If you double your bet, your expected loss is now ($2*47%)+(-$2*53%) which is about -$.11 (no surprises that your expected loss doubles each time you double your bet).  So, doubling your bet doesn’t help you in the long run!  But, this doesn’t translate perfectly to the strategy as we will see.

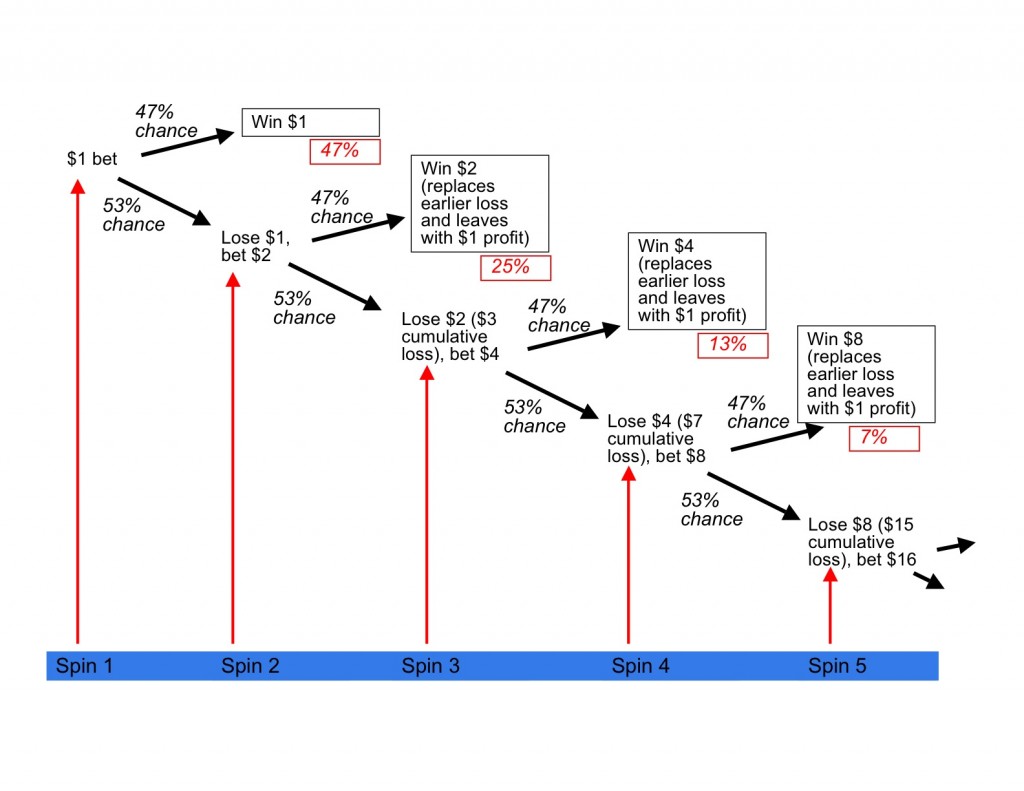
Your probability of winning that second spin and thus recouping your losses is only 47%.  But, you only have to spin this second time if you had lost previously.  So, while the second spin is an independent event (meaning that whether the ball lands on red, black, or 0, 00 the first spin has no bearing on where it lands the second), you are only spinning if you lost the first time.  To illustrate this, see the below tree of potential outcomes.

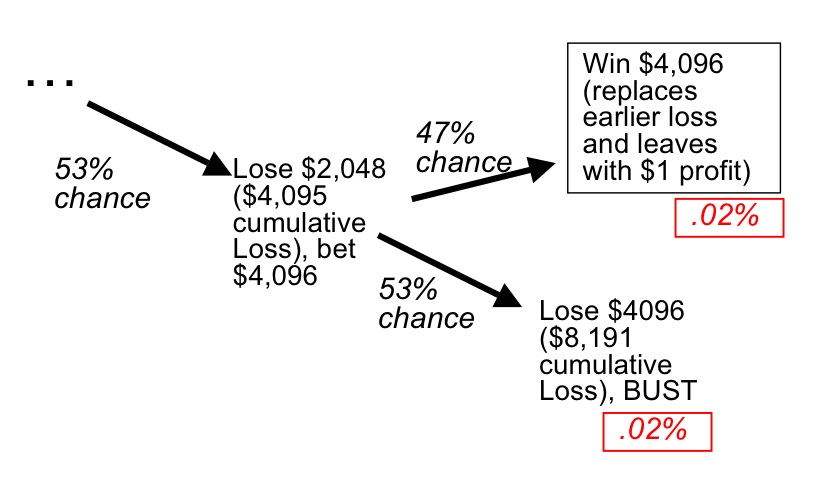
The above tree displays the following series of events: we start with a $1 bet, there is a 47% chance that we win and make a $1 profit.  There is a 53% chance we lose.  If we lose, we double our bet and there is a 47% chance we win and recoup our losses and make a $1 profit.  There is a 53% chance we lose again and then have to double our bet again and so on.  The red boxes are the probability of any given outcome occurring.  All of the outcomes in the black boxes recoup our losses and yield $1 profit.  Below is what the final piece of the decision tree would look like assuming our limiting factor (a table maximum bet) is $5,000:

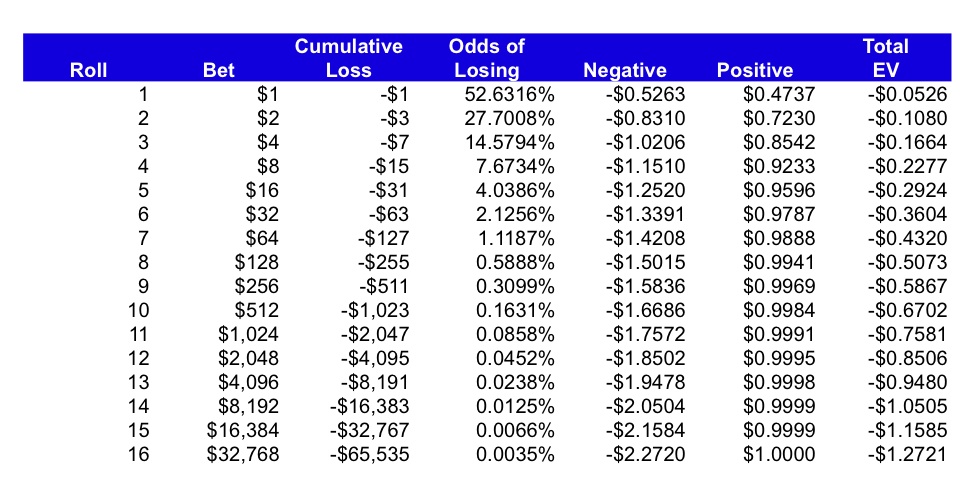
We can see that the chances of either of the two outcomes in our 13th spin actually happening when we start is very low – only about 2 basis points (a basis point is a percent of a percent, also abbreviated as bps, 100 bps = 1%).  So, we can agree by looking at the outcome tree that all outcomes besides the BUST scenario yields a $1 profit.  Therefore, our expected value calculation is ($1 * the chances of us not going bust) + (-(value of final bet + accumulated losses) * chances of getting to this outcome).  In our scenario, the equation is as follows: ($1 * 99.98%) + (-($4,095+$4,096)*.02%) = -$0.85.  So, each time we put our initial $1 bet on the table, we could expect to lose $0.85.

The previous post concluded that after 10,000 nights in a casino, employing a similar strategy, one could very well walk away a winner.  Of course, here we see that our chances of losing our shirt are .02%, or 1 in 5,000 iterations (where an iteration is each time you start over with a $1 bet).  So, in 10,000 nights, it is very possible for us to get lucky and never hit the BUST scenario where we lose all of our money.  The conclusion is that, if you can find a casino that will allow you to employ this strategy, you may just get lucky in the short term and make some money.  Personally, I’d rather play craps!

Here is a table which provides some detail on how your expected payoff can change depending on how far you push it.  The ‘Negative’ column = the chances of losing * -(cumulative losses + current bet).  The ‘Positive’ column = the chance you don’t go bust * $1.  The excel is downloadable at the end of the post.

Hopefully this post clears up a few things about the previous one, and also sheds some light on basic probability models and how one would think about proving the validity of this strategy outside of the monte carlo simulator presented in the past post.  I also hope I will write more posts on open bars in the future, as opposed to ones with so many excel/powerpoint graphics!

Roulette pt 2 math